PGI-15 Tutorial

Spiking Neural Networks

Neuron modeling

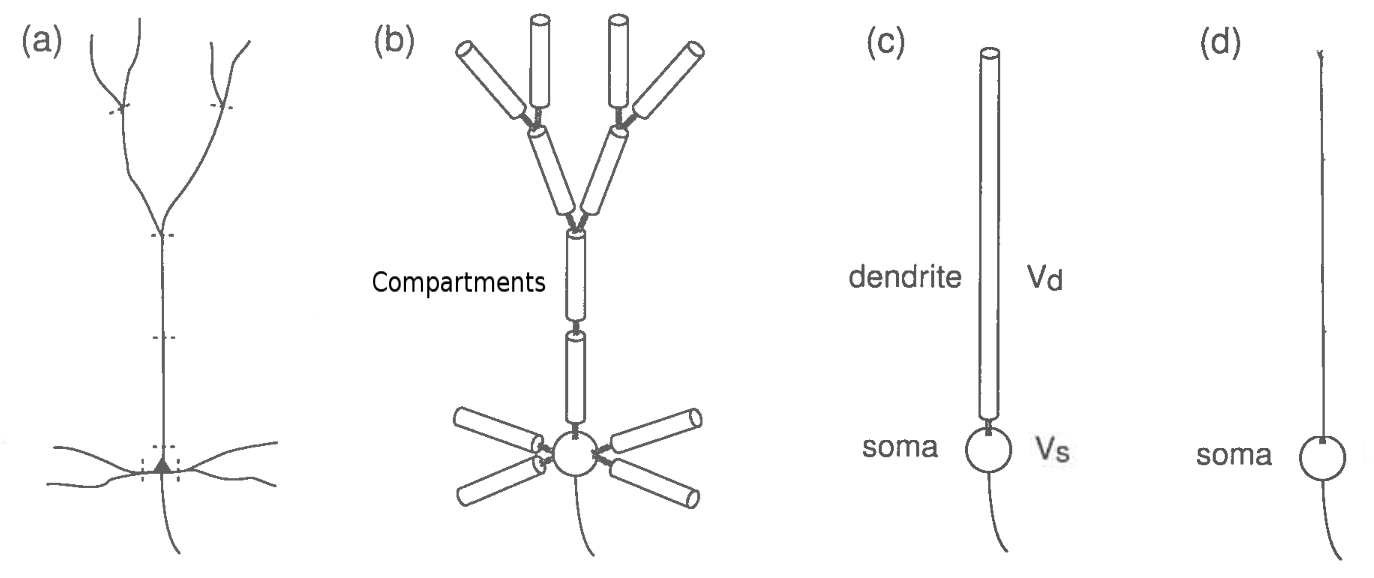
For simplicity, computational neuroscientists often approximate neuron dynamics with one or more point compartments

Point Neuron Models

Everything should be made as simple as possible, but not simpler. - A. Einstein

Point Neuron Models

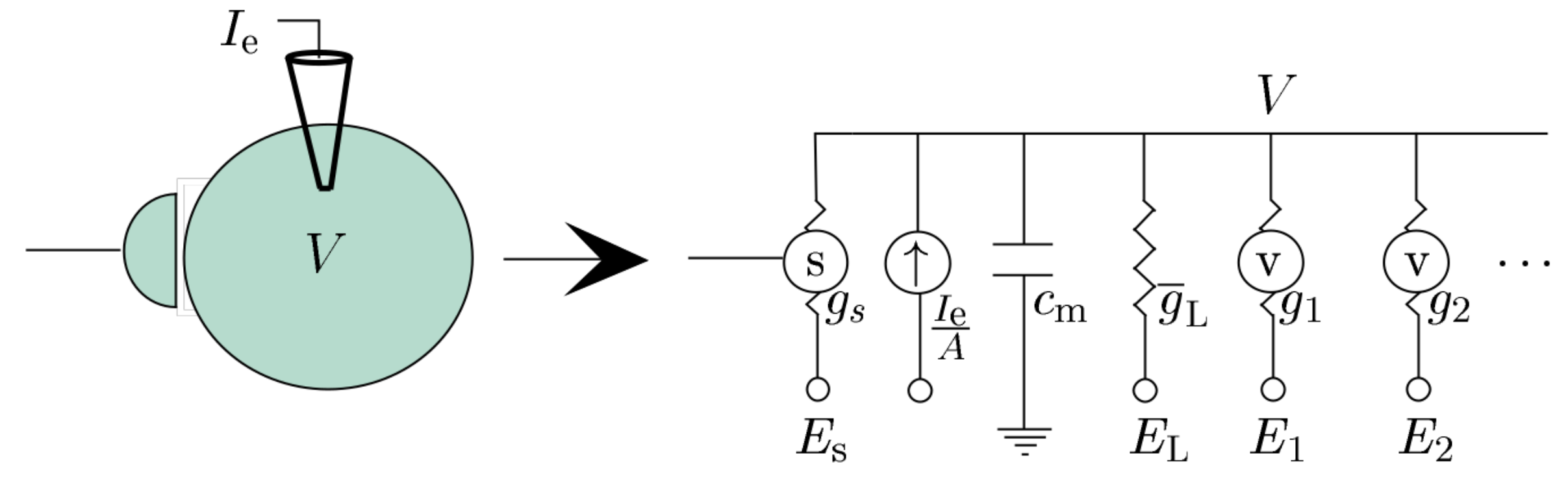
Dayan and Abbott, 2001

Equivalent Circuit of the neuron:

Leaky Integrate & Fire Neuron

• Integrate-and-fire Neuron Dynamics \[ \begin{split} C \frac{\mathrm{d}}{\mathrm{d}t}u &= - g_L u + I_{syn} + I_{ext} + noise\\ \text{if $u>\theta$}&: \text{ elicit spike,} \text{ and } u \leftarrow u_r\text{ during $\tau_{arp}$}\\ \end{split} \]
  When $u$ reaches $\theta$, an action potential (spike) is elicited. After this, the membrane potential is clamped to the reset potential $u_{r}$ during an absolute refractory period $\tau_{arp}$.
• Current-based Synapse Dynamics \[ \begin{split} \tau_{s} \frac{\mathrm{d}}{\mathrm{d}t}I_{syn} &= - I_{syn} \\ \text{on presynaptic spike}&: I_{syn} \leftarrow I_{syn}+w \end{split} \]
  Each incoming spike results in a post-synaptic current that rises instantly and decays exponentially.

Dayan and Abbott book, Section 5.4 and 5.8

Leaky Integrate & Fire Neuron

\[ \begin{split} C \frac{\mathrm{d}}{\mathrm{d}t}u &= - g_L u + I_{syn} + I_{ext} + noise\\ \text{if $u>\theta$}&: \text{ elicit spike,} \text{ and } u \leftarrow u_r\text{ during $\tau_{arp}$}\\ \end{split} \] \[ \begin{split} \tau_{s} \frac{\mathrm{d}}{\mathrm{d}t}I_{syn} &= - I_{syn} \\ \text{on presynaptic spike}&: I_{syn} \leftarrow I_{syn}+w \end{split} \]

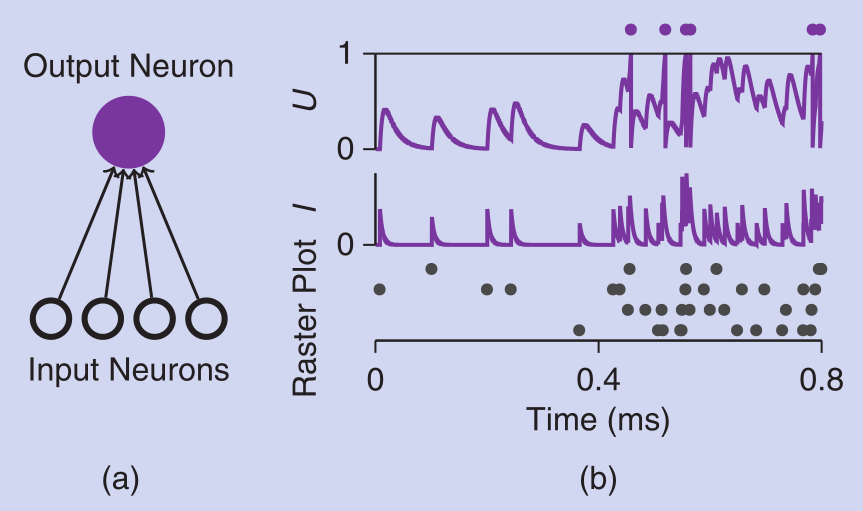
Spike Trains

• Times at which the neuron spikes: $t_1, ..., t_N$.
• Mathematical formulation of a spike train: \[ s_{pre}(t) = \sum_{k=1}^N \delta(t-t_k) \] where $\delta$ is the delta Dirac: \[ \int _{-\infty }^{\infty }\delta (x)\,dx=1 \]

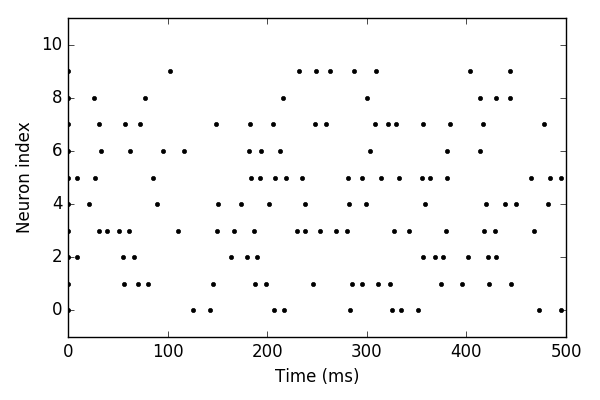
• The synaptic current is then given by: \[ \begin{split} \tau_{s} \frac{\mathrm{d}}{\mathrm{d}t}I_{syn} &= - I_{syn} + w s_{pre} (t)\\ \end{split} \]

Firing Rates and Rate-Coding

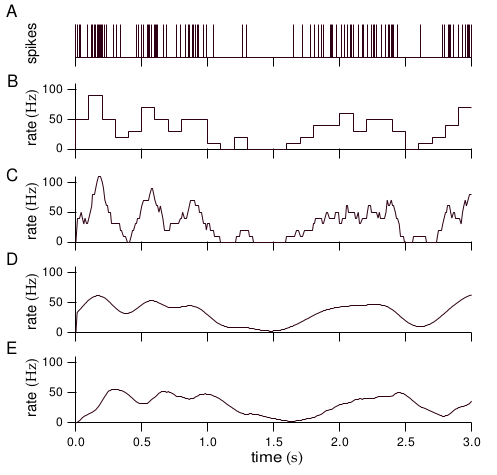
• Mean Firing rate or Spike-Count \[ \frac{1}{T}\int _{0 }^{T }\mathrm{d}t\, s_{pre}(t)= N/T = r \]
• Discrete-time firing rate obtained by binning time and counting spikes (B)
• Using a window function $h(t)$ (C,D,E) \[ \int _{0 }^{T } \mathrm{d}t\, h(t) s_{pre} = r(t) \]
• In the rate code, the information is coded in r(t)
• Rate codes are robust to variations in spike times

Receptive Field and Population coding

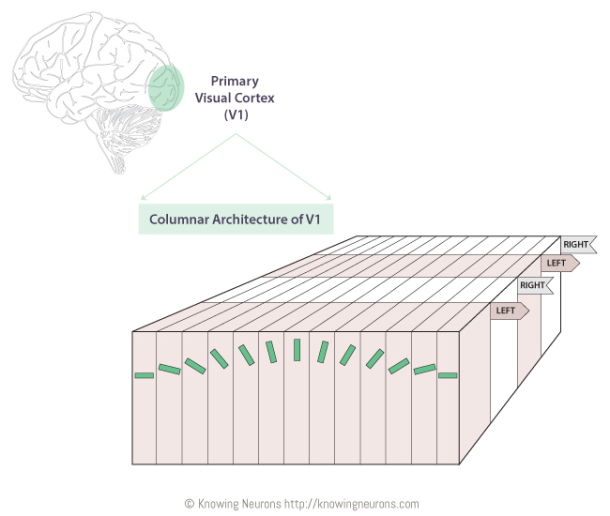
Representation of information distributed across the firing rate of multiple neurons

Tuning Curves

Hubel andWiesel, 1968

Reliability in Spike Timing

Mainen and Sejnowski, 1995

Spike-Time Coding

• Evidence that spike times in early sensory areas are very precise (locked to sensory stimuli)
• The Interspike interval (ISI) is: \[ ISI_k = t_{k} - t_{k-1} \]
• The precise timing of the neurons, i.e. ISIs, carry most of the information
• Higher information rate $\rightarrow$ faster response, but not robust to variation
• In the timing code, the information is coded in the interspike intervals

Firing Code vs. Spike-Timing Code

• Whether the brain uses a spike code or rate code is still hotly debated.
• Solution: use models that are consistent with both
• Both modes can be modeled as the two extremes of an instantenous firing rate r(t) defined as: \[ r(t) = P(s_{post} = 1 | s_{pre}) = P(s_{post} = 1 | u(t) ) P(u(t) | s_{pre}) \]
• Timing code: High $P(s_{post} = 1 | s_{pre})$ around spike times otherwise very small ($\rightarrow 0$)
• Rate code: constant $P(s_{post} = 1 | s_{pre}) = \bar{p} $
• When does the brain use timing and rate?

An important aspect of encoding is response variability

Firing Rate of a Leaky Integrate & Fire Neuron

Firing rate neurons are the building blocks of artificial neural networks

End