PGI-15 Tutorial
Artificial Neural Networks
02.11.2023 | Emre Neftci, Susanne Kunkel, Jamie Lohoff, and Willem Wybo
The First Artificial Neuron
-
In 1943, Warren McCulloch and Walter Pitts propose the first artificial neuron, the Linear Threshold Unit.
$f$ is a step function: $$ y = \begin{cases} f(a) &= 1\text{ if } \ge 0\\ f(a) &= 0\text{ if } a< 0\\ \end{cases} $$
$a$ is a weighted sum of inputs $x$
- "Modern" artificial neurons are similar, but $f$ is typically a sigmoid or rectified linear function
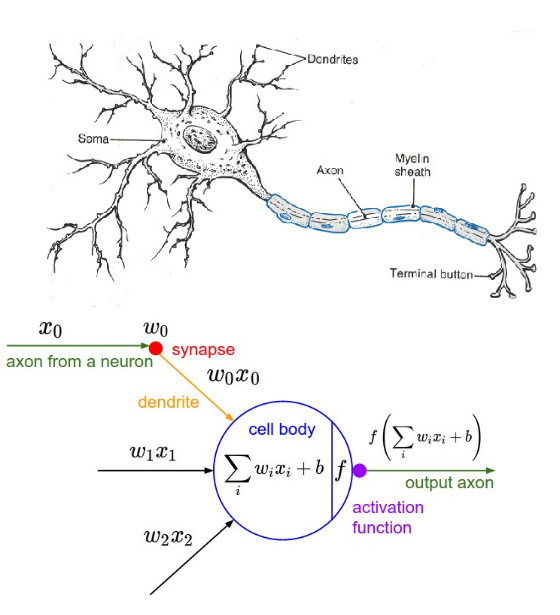
Mathematical Model of the Artificial Neuron

- $x_i$ is the state of the input neurons
- $w_i$ is the weight of the connection
- $b$ is a bias
- The total input to the neuron is: $ a = \sum_i w_i x_i +b $
- The output of the neuron is: $ y = f(a) $
- where $f$ is the activation function
The Perceptron
- The Perceptron is a special case of the artificial neuron where: \[ \begin{eqnarray} \mbox{y} & = & \begin{cases} -1 & \mbox{if } a = \sum_j w_j x_j + b \leq 0 \\\\ 1 & \mbox{if } a = \sum_j w_j x_j + b > 0 \end{cases} \end{eqnarray} \]
- Three inputs $x_1$, $x_2$, $x_3$ with weights $w_1$, $w_2$, $w_3$, and bias $b$
Perceptron Example
-
Like McCulloch and Pitts neurons, Perceptrons can be hand-constructed to solve simple logical tasks
Let's build a "sprinkler" that activates only if it is dry and sunny.
Let's assume we have a dryness detector $x_0$ and a light detector $x_1$ (two inputs)
Find $w_0$, $w_1$ and $b$ such that output $y$ matches target $t$
| Sunny | Dry | $a$ | $y$ | $t$ |
|---|---|---|---|---|
| 1 (yes) | 1 (yes) | 1 | ||
| 1 (yes) | 0 (no) | 0 | ||
| 0 (no) | 1 (yes) | 0 | ||
| 0 (no) | 0 (no) | 0 |
| $w_0 =$ 0 | $w_1 =$ 0 | $b =$ 0 |
Logic Gates
-
Logic gates are (idealized) devices that perform one logical operation
Common operations are AND, Not, and OR and can perform Boolean logic
Using only Not AND (NAND) gates, any boolean function can be built.
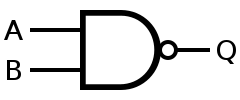
| INPUT | OUTPUT | |
| A | B | A NAND B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Thus: Any Boolean function can be built out of Perceptrons!
Linear separability
A perceptron is equivalent to a decision boundary.
A straight line can separate blue vs. red

There is no straight line that can separate blue vs. red
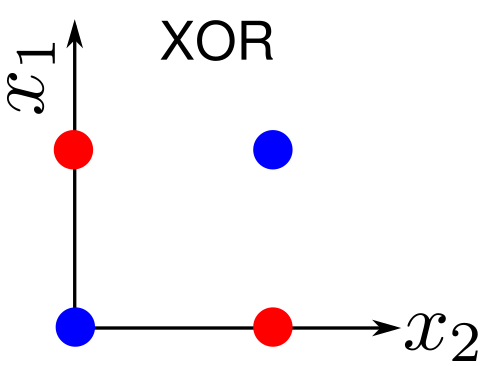
Problems where a straight line can separate two classes are called Linearly Separable
Perceptron learning algorithm to learn to classify linearly separable points
Optimization Algorithm Gradient Descent
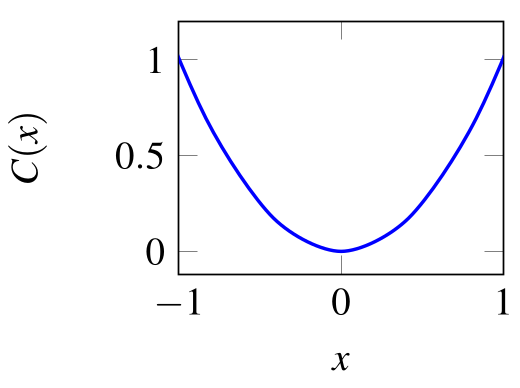
-
Example: Find $x$ that minimizes $C(x) = x^2$
Incremental change in $\Delta x$:
$$
\begin{eqnarray}
\Delta C \approx \underbrace{\frac{\partial C}{\partial x}}_{\text{=Slope of }C(x)} \Delta x
\end{eqnarray}
$$
Gradient Descent rule: $\Delta x = - \eta \frac{\partial C}{\partial x}$, $\Delta C \approx - \eta \left( \frac{\partial C}{\partial x} \right)^2$
Gradient Descent for finding the optimal $x$:
$
\begin{eqnarray}
x \leftarrow x - \eta \frac{\partial C}{\partial x}
\end{eqnarray}
$
Linear separability
A perceptron is equivalent to a decision boundary.
A straight line can separate blue vs. red

There is no straight line that can separate blue vs. red

Problems where a straight line can separate two classes are called Linearly Separable
Most complex problems are not linearly separable
Deep neural networks
How many hidden layers and how many units per layer do we need? The answer is at most two
Hertz, et al. 1991
Szegedy et al. 2014
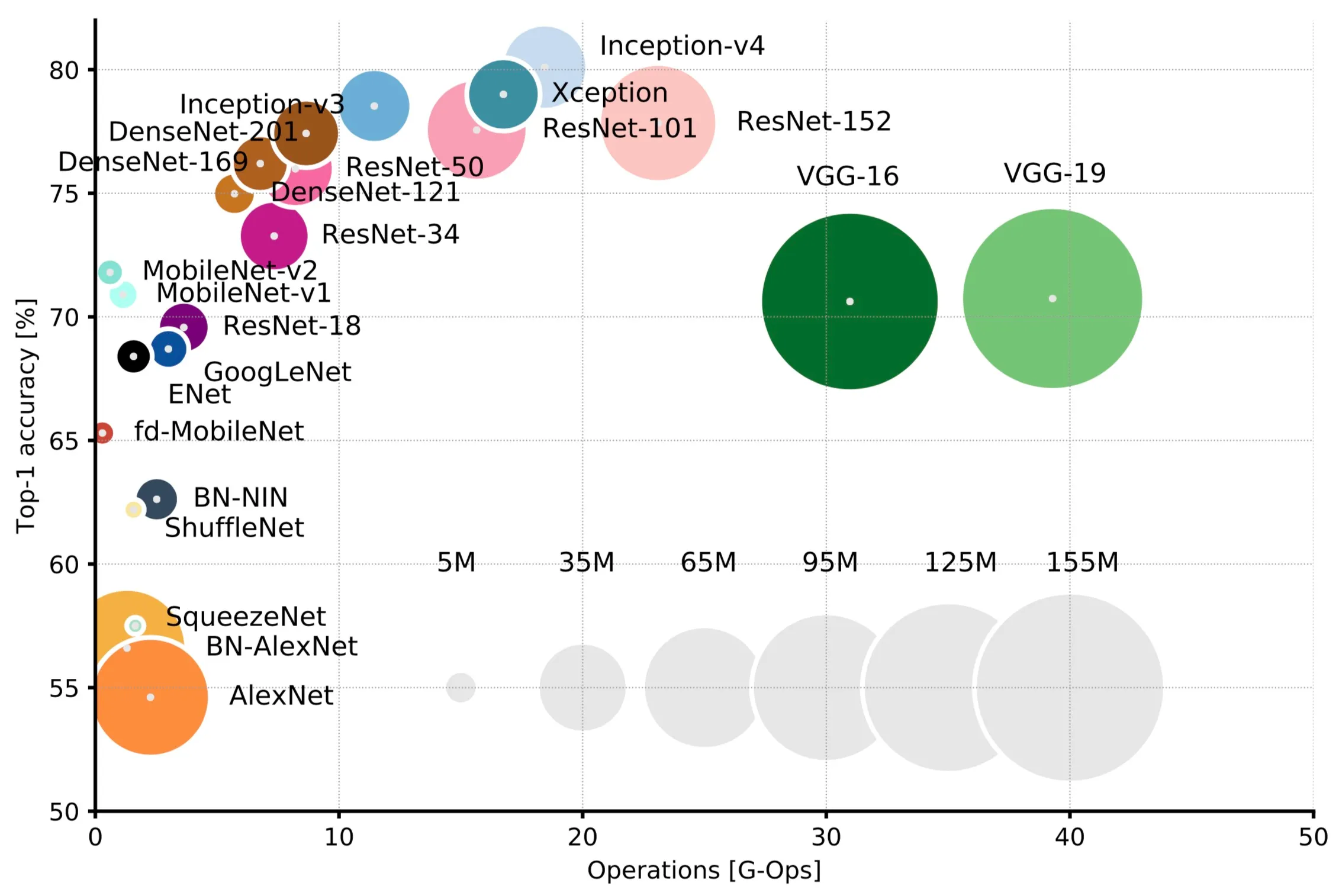
Canziani et al. 2018
Single Layer Network with Sigmoid Units M
- Weight matrix: $W^{(1)} \in \mathbb{R}^{N\times M}$ (meaning $M$ inputs, $N$ outputs) $$ \begin{eqnarray} y^{(1)}_i &=& \sigma(\underbrace{\sum_j W^{(1)}_{ij} x_j}_{a_i^{(1)}}) \\ \end{eqnarray} $$
- MSE cost function, assuming a single data sample $\mathbf{x}\in\mathbb{R}^{M} $, and target vector $\mathbf{t}\in\mathbb{R}^{N}$ $$ C_{MSE} = \frac{1}{2} \sum_i(y^{(1)}_i - t_i)^2 $$
- Gradient w.r.t. $W^{(1)}$ (in scalar form): $$ \frac{\partial }{\partial W^{(1)}_{ij}} C_\text{MSE}= (y^{(1)}_i - t_i) \sigma'(a^{(1)}_i) x_j $$
Two Layer Network with Sigmoid Units
- Two layers means we have two weight matrices $W^{(1)}$ and $W^{(2)}$
- $W^{(1)} \in \mathbb{R}^{N^{(1)}\times M}$, $W^{(2)} \in \mathbb{R}^{N^{(2)}\times N^{(1)}}$
- The output is a composition of two functions:
-
Cost function $ C_{MSE} = \sum_{i=1}^{N^{(2)}}(y^{(2)}_i - t_i)^2 $
Gradient wrt $W^{(2)}$ is: $ \frac{\partial }{\partial W^{(2)}_{ij}} C_\text{MSE}= \underbrace{(y^{(2)}_i - t_i) \sigma'(a^{(2)}_i)}_{\delta^{(2)}_i} y^{(1)}_j $
Gradient wrt $W^{(1)}$ is: $ \frac{\partial}{\partial { W_{jk}^{(1)}}} C_{\text{MSE}} = \underbrace{(\sum_i \delta_i^{(2)} W^{(2)}_{ij}) \sigma'(a^{(1)}_j)}_{\text{backpropagated error}\, \delta^{(1)}_{j}} x_k $
This is a special case of the gradient backpropagation algorithm
